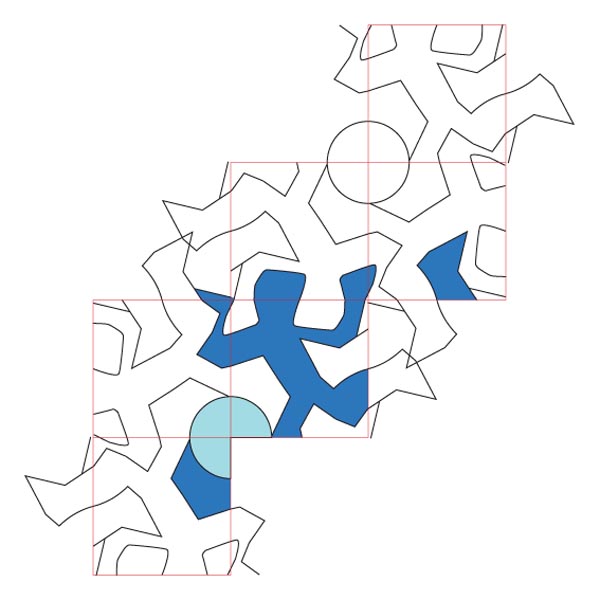
様々な多面体をベースにしたテセレーションの球体への拡張 (クリックで拡大表示)

アノマロカリス
(ベース:正8面体の応用)

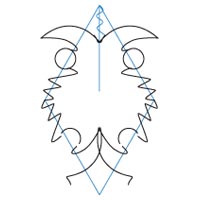
1面のデッサン

4分の1球体展開図

古代魚
(ベース:菱形12面体)

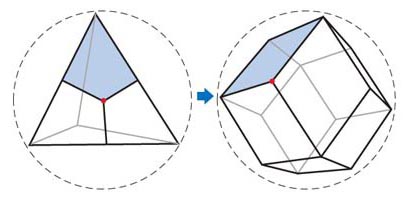
正4面体:双対:菱形12面体

カエル
(ベース:菱形12面体)

1ピース

ワニ
(ベース:凧形24面体)

球体:下図モデル

石膏:マスターモデル

恐竜
ベース:凧形24面体

恐竜-2
ベース:正4面体

鷲とウサギ
ベース:凧形24面体

ピース

マンモスと狩り
(ベース:凧形24面体)

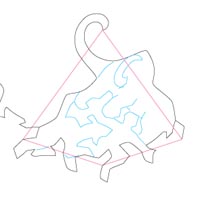
下図モデル

戦士
(ベース:正6面体)

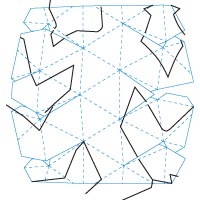
6分の1球体展開図

2パーツ裏面

サンタ
(ベース:正6面体)

ピース

龍の玉と玉の龍
(ベース:ねじれ双4角錐)

龍と玉

猫
(ベース:変形立方体)

犬
(ベース:変形立方体)

馬
(ベース:菱形12面体)

トカゲ
(ベース:凧型24面体)

猿
(ベース:菱形12面体)

サソリ
(ベース:ねじれ双6角錐)

カメレオン
(ベース:並進5分割)

カメレオンパーツ

多面体で閉じた図形にするには平面と同様に隣り合う全ての面と隙間無く連続させなければならないが、多面体では平面の場合の敷き詰めルールが適応されない場合もある。それは多面体の展開図が敷き詰め可能かどうかを検証すれば解る。 例として、立方体の場合では以下の様になる。この場合は平面では敷き詰められないことが解る。
多面体テセレーションを球体に拡張する場合は、面の数が少ない程変形率は大きくなる事を考慮して作図しなければならない。

To create a closed figure with a polyhedron, all adjacent faces must be continuous with no gaps, just like with a plane, but with polyhedrons, the tiling rules for planes do not always apply. This can be seen by verifying whether the developed diagram of the polyhedron can be tiled. As an example, the case of a cube looks like this. In this case, it is clear that it cannot be tiled on a plane.
You must consider the distortion when the tessellation that drawn on the polyhedron extend to sphere tessellation, It is distorted Larger than the original image of polyhedron.